SASMO新加坡数学竞赛初中部,学霸用这个方法拿到高分,值得学习
题一、
化简:³√(10+6√3)−³√(10−6√3)

分析题目
双重三次根式之差,比较复杂,直接凑和的立方,似乎难度太大了,没法进行下去,那这种我们只能转换思路,通过引入参数,来构建方程组,通过解方程来解决
参考答案

题二、
求:((−1−√5)/2)⁶的整数部分是多少?

分析题目
整数解问题,显然需要的是两边夹,限定范围,枚举验证,本题也是这个思路,不过本题存在6次方,那我们首先需要将此无理数化为最简二次根式,才能进行分析
参考答案

题三、
已知x,y为正实数,且满足11x²−48xy−35y²=0
求(3x−y)/(x+2y)的值

分析题目
已知的是一个二元二次方程,直接解方程,肯定是解不出来,仔细分析所求代数式,分子分母都是一阶齐次代数式,再回头看已知条件,为二阶齐次多项式,这种已知和所求都是齐次的情况下,最简单高效的处理方式就是归一化
参考答案

题四、
化简:√2(√(3+√5)−√(3−√5))

分析题目
双重根式化简,那显然是要凑完全平方式,但本题是两个根式下面的式子为共轭式,那更简洁高效的解法就是平方再开方
参考答案
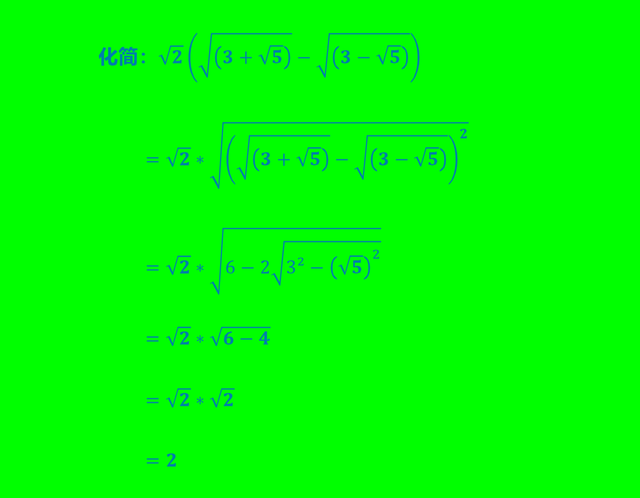
题五、
已知a,b,c是方程x³−x²+1=0的三个解
求:a²/(bc)+b²/(ac)+c²/(ab)

分析题目
我们首先看下所求的代数式,口算即可发现,三个分式通分后,分母就是三元积,分子就是三元立方和,那也就是说,我们要求得三元积的值,以及三元立方和的值,再分析已知条件,一元三次方程的三个根,那显然是考察我们对一元三次方程,韦达定理的熟悉程度了,这个需要掌握,不熟悉的话,直接展开也是可以得到的
参考答案

#大有学问# #家长百问百答# #学问分享官# #深圳本地# #2022知识来盘点#
















评论