AEIS考试几何专项训练,请在45分钟内完成答题

新加坡滨海湾
参加新加坡AEIS考试的考生,经过前期紧张的备考,在最后一个阶段要改变一下策略,进行专项复习。这样可以进一步巩固知识,揪出知识盲点,然后进行有针对性的强化训练。本次我们的突击重点是几何圆形的部分。
由于各位同学要用英文参加考试,我们就不翻译成中文了,强迫自己尽快熟悉英文。
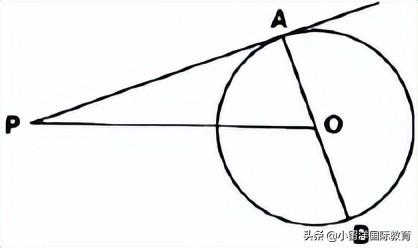
1. In the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB = 115° then find ∠APO.
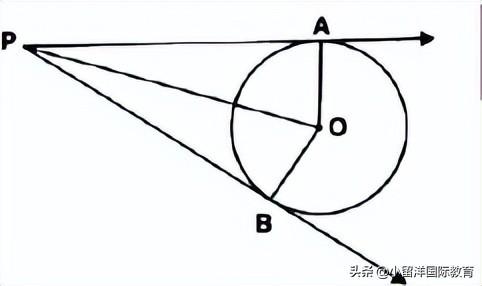
2. In the following figure, PA and PB are tangents drawn from a point P to the circle with centre O. If ∠APB = 60°, then what is ∠AOB?
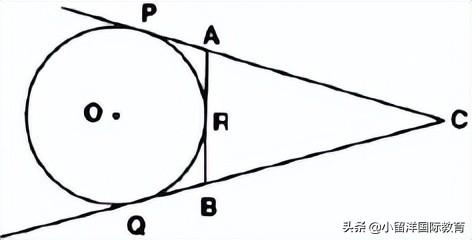
3. In the figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If QC = 11 cm, BC = 7 cm then find the length of BR.
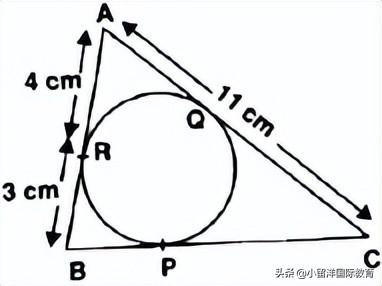
4. In the figure, △ABC is circumscribing a circle. Find the length of BC.
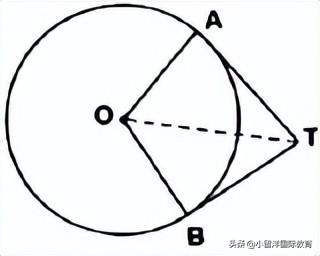
5. In the figure, if ∠ATO = 40°, find ∠AOB.
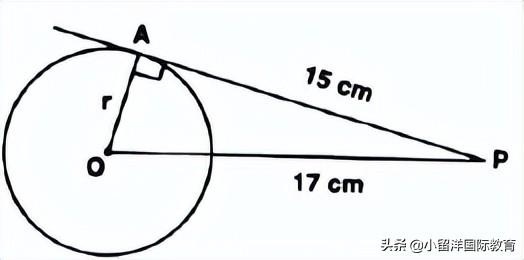
6. From a point P, the length of the tangent to a circle is 15 cm and distance of P from the centre of the circle is 17 cm, then what is the radius of the circle?
7. The two tangents from an external point P to a circle with centre O are PA and PB. If ∠APB = 70°, then what is the value of ∠AOB?
8. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
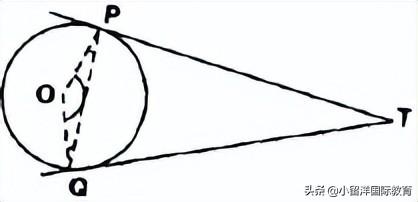
9. A circle is touching the side BC of a ��ABC at P and touchign AB and AC produced at Q and R. Prove that:
![]()
10. In two concentric circle, a chord of the larger circle touches the smaller circle. If the length of this chord is 8 cm and the diameter of the smaller circle is 6 cm, then find the diameter of the larger circle.
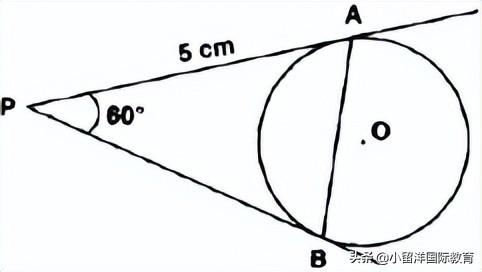
11. In the following figure, PA and PB are two tangents drawn to a circle with centre O, from an external point P such that PA = 5 cm and ∠APB = 60°. Find the length of chord AB.
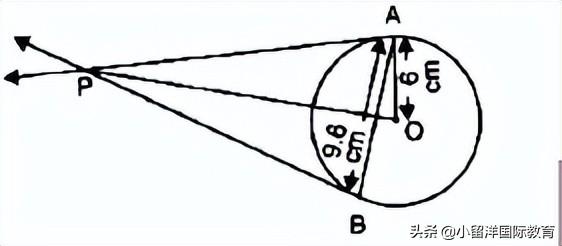
12. In the following figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length PA.
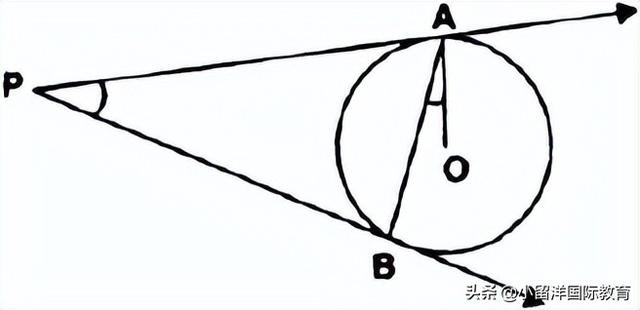
13. Two tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB = 2∠OAB
14. ABC is an isosceles triangle, in which AB = AC, circumscribed about a circle. Show that BC is bisected at the point of contact.
15.Two tangents PA and PB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
欢迎大家在评论区讨论。➥ 关注「小留洋」,一起研究海外数学题。





















评论