孩子“计算渣”？让孩子刷题之前我劝你先做这件事

C妈 CE爸妈学堂

今天的文章，C 妈想问大家一个小问题：你是怎么教娃算算术的？

为什么突然想到这个问题呢？

因为前几天，办公室有个同事说：她家娃正在学10以内的加减法，但是，任你怎么掰开了揉碎了讲，孩子就是不开窍。

结果，一气之下，她把十以内的加减法全部给孩子列了出来，让孩子像背九九乘法表那样背下来……

说到计算呢，它绝对算不上难，但是绝对能算得上学习中的头等大事。

虽然，后期应该没有人能纯靠计算甩下别人几条街，但是，计算绝对算得上兵家必争之地！

计算能力强未必是数学学霸，但是计算能力弱必然成为数学学渣。

虽然各个年龄段的孩子在计算中都有不同程度的问题，但是造成问题的成因却不太一样。

今天，C妈就来和大家好好说说计算中的鸡毛蒜皮！

4-6岁

这个年龄段的孩子计算总出错，最大的原因大概率是根本不明白数字、加法、减法……等一系列数学符号到底是个啥！

就像咱们开篇提到的，同事家的小孩学不会计算，最终直接简单粗暴地背下来。

不满大家说，CC当初刚接触加减法的时候我也这么干过。

刚开始的时候，还觉得挺有用的。

全都背下来之后，超过别的孩子一大截呢！

但是，弊端也很快地显现出来了：

有一次，CC做了这么一道题，大概意思是：小明有6块糖，妹妹拿走了2块，问小明还剩几块糖。

当时CC写的算式是：2+4=6，小明还有4块。

这答案，没毛病，但这逻辑着实有点奇怪啊……老母亲简直不知道该哭还是该笑……

这明明是一道减法题好吗？

我也是后来才知道，原来是我们一直让她背加法算式，让她形成了惯性思维。

她一看见2、6这两个数字，惯性思维就驱使她想到2+？=6。

所以，她列出这样的算式也就不足为奇了！

我们总是认为，加法和减法相辅相成，加法会了，减法自然不用愁。

明白了加法的底层逻辑，减法的确是不用愁了。

但我们却忽略了最重要的一点：会背加法算式≠明白加法的底层逻辑。

对于数学学习而言，死记硬背肯定是走不长远的，理解才是其中的精妙之处啊！

所以，对于这个年龄段的小朋友来说，我们最重要的就是要帮助他们弄清楚数是什么，和运算中最最基本的逻辑。

这一点直接就有现成的参考方法，就是新加坡的CPA教学法。

这种教学方法已经有很长的渊源了，最早是由美国心理学家Jerome Bruner在19世纪60年代提出的，他经过观察发现，小孩子的学习，往往会经历三个阶段，分别是：

• C - Concrete 具象化
• P - Pictorial形象化
• A - Abstract 抽象化

在幼小衔接阶段，如果能做好前两步，就已经能解决孩子学习中90%以上的问题啦！

所以，今天C妈重点跟大家说说前两步。

01具象化

让数字/运算法则以孩子看的见的方式呈现

最简单的方法就是掰手指。

比如：3+2=5

就可以让孩子先伸出3根手指，再伸出2根手指，然后把两个手和一起，从1开始数，12345，最后等于5。

三根手指代表3，2根手指代表2，所有的手指和在一起一共是5。

3根手指代表数字“3”，2根手指代表数字“2”，两个手合在一起代表“+”。

多么典型的把抽象的数字变成孩子可以看见的方式啊。

把手指换成别的小东西，是同样的道理。

其实生活中就有很多帮助孩子把数学符号具象化的机会。

数字具象化：

卧室里有1张床、2个床头柜、床头柜上有3本书；

数一数，我们前面有几个人在排队；

数一数，餐桌前有几把椅子……

加减法具象化：

CC有2块糖，奶奶又给了她一块，手里的糖变多了，这就是加法。

她吃了一块糖，手里的糖变少了，这就是减法。

说到底，加减法就是某个集合中的个体拿来/拿走的过程，让孩子感受到这个过程就是帮孩子具象化加减法的过程。

这个阶段就是把抽象的数学符号用孩子看得见摸得着的方式展现在孩子的眼前，以便孩子可以直观地理解各个事物之间的关系。

这样才算是符合孩子的心理发展规律。

但是，如果长时间停留在这个阶段，孩子的数学不会有质的提升，甚至还会产生误解，以为数字和实物是一回事。

因此，为了让孩子真正“开窍” ，在具象化的学习之后，要促使他们进入下一个阶段，而这个阶段也就是CPA教学法的精髓——形象化。

02形象化

让孩子通过绘画建模，把数学问题“可视化“！

在国内，实际上很多幼儿园在中班后期的时候就开始逐渐“建模”了，只不过前期比较简单，还是会结合一些具体事物来一步步过度。

比如：学习数字泡泡，这非常有助于以后的加减法。

前边的一个泡泡代表总和，它的数量和前边的图形数量一致，而图形中又有白色和灰色，虽然是抽象的图形，但也直观地展示了数量。

这一步是为了帮助孩子更好地从具象化向形象化过渡。

这一步做好之后就要开始真正的“建模”了！

先举个简单的例子吧，比如书中的对比，谁多谁少？

用在加法上，比如，小明有3个橘子，玲玲有4个橘子，两人一共有几个呢？

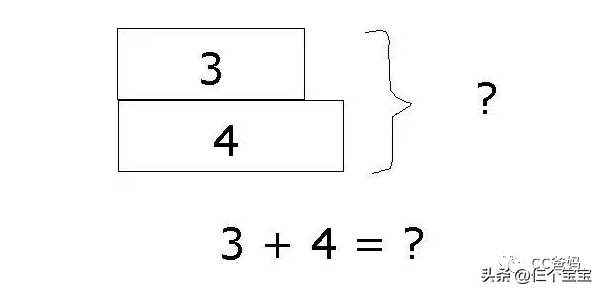
经过这样的训练，孩子看到的虽然不是具体的实物，但题目依然可以比较直观地呈现在孩子眼前。

这样孩子在比较多少，选择加法还是减法的时候都会有比较明确的思路，困难也会小很多。

孩子再大点建模的方式还可以应用到更多的领域上：

比如：

理解分数：

百分比：

乘法……

可以说建模的方式可以贯穿整个小学的数学学习中。

所以说，建模的方式用好了，孩子就可以顺利进入真正的抽象数学的学习。

而在这一步打好的坚实基础，更是可以让孩子们培养出强烈的“数感”，为接下来学习更加抽象的代数方程、立体几何等等做好准备。

对于刚开始接触加减法的孩子来说，弄明白数字的真正含义，理清底层逻辑，计算也就成功了一半了。

但是，孩子大了呢，数和量已经完全对应，也理解加减法的基本逻辑，在计算上还是没少出错啊。

7-9岁

这个年龄段的孩子，频繁出现计算问题，可以试试以下几个方法！

1、督促孩子规范书写

规范书写在语文中的重要性，咱就不多说了。

在数学学习上，如果书写潦草的话，不仅给别人带来烦躁的感觉，也会给自己埋下很多雷。

比如：

有的孩子写的0和6、7和1等不够规范，写完了自己都忘了，到底是啥了；

还有人写32-11，很容易写成32+1；

再比如：

列竖式的时候像这样对不齐：

如果有这样的情况的话，咱们就要注意提醒，督促孩子规范书写，这样才能从根本上保证计算的正确率。

还有一种书写的情况，就是演算纸上的空间分配不均。

我就曾经看见过CC的一个同学，演算纸那个省啊。很多数字都是挤在一起的，这样就会导致孩子好不容易算对了，却抄错了答案。

得不偿失。

所以，我们可以从孩子开始用验算纸的时候就有意识地教他，把演算纸分成不同的区域。

我是这样告诉CC的：

把演算纸折叠成四个区域：

每个类型的题在不同的区域验算，这样既不会很紧凑，还能在最后检查时一目了然，这个区域是哪些题。

降低检查的工作量。

2、用正确的方法验算

虽然C妈的数学水平绝对算得上文科中的学霸，但是，说实话，我上小学的时候最讨厌的一件事就是验算。

每次看见那种列竖式计算并验算的题目，我都超级脑瓜疼。

后来长大了才知道，原来验算真的不一定中规中矩的再算一遍，有很多很巧妙的方法就可以一眼看出那些很明显的错误。

比如：

只算个位：

现在的孩子们也就是学加减法的阶段吧！

所以验算的时候，我们就可以教孩子只算个位，个位数的加减法就简单多了吧！

比如：

18+17，8+7=15，个位上肯定是5，那如果不是5的话，肯定就错了。

还可以估算：

就拿咱们前面举的对齐的例子来说，123+26，因为没对齐，把答案错写成383。

那我们就想，100多加上20多，怎么着也不能是300多吧。

所以很轻松就能看出来答案是有问题的。

尤其是在考试的时候，这样的验算方法可以覆盖到更多的题目，纠出更多的低级错误，从而提升准确率。

不至于，试卷一发下来，就感叹，这是因为粗心。

逆向思维验算：

如果真的需要全面的检查一遍的话，那也不要完全按照原来的套路算第二遍。

因为把原来的道路重新走一遍，是非常容易出现一模一样的错误的。

我们要用逆向思维。

原来是加法的我们就用减法验算，原来是减法的就用加法。

这样验算，才能更准确的检查出错误。

C妈说：计算能力好的孩子不一定数学好，但是计算能力不好的孩子数学是一定不会好的。如果一开始孩子承受的就是挫败感的话，很容易让孩子对一门学科失去兴趣。但是，就算是现在孩子的计算总出错，甚至是有点渣，咱们也别着急。慢慢地帮孩子找找原因，逻辑不清的理逻辑，书写潦草的规范书写……找对了原因，再适当刷题辅助。这样才能更有效地帮助孩子提升计算的准确率。