基于因数分解,解新加坡数学竞赛SASMO试题,形成一类题思维定式
SASMO2021-G4-Q18:一个长方体在它的6面都被涂了色,将它分成54个小长方体,问至少有多少个小长方体,它们至少有两面是涂色的?
看到这个题,首先要思考如何切分?需要先将54进行因数分解:
54=2*27=2*3*3*3。
由此,可以看出,切分方法有两种:
第一种:54=6*3*3;
第二种:54=2*3*9。
按照第一种切分方法,参见下图。
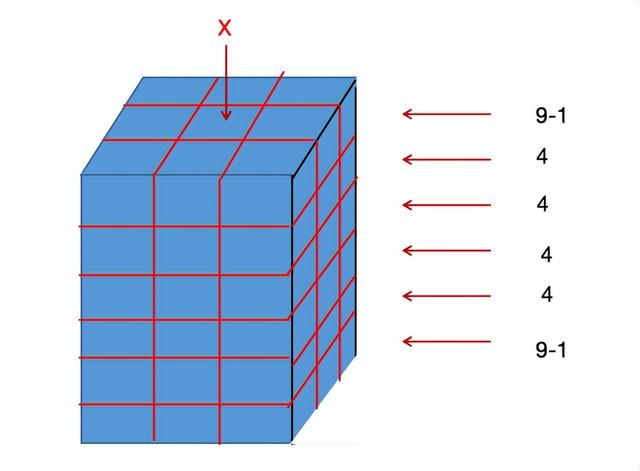
共计32个小长方体有两面以上涂色。
类似地,按照第二种切分法,共计40个小长方体有两面以上涂色。所以取其较少的那种切分法,最终答案为32。
很多题目中,都会用到因式分解或因数分解,特别是小学阶段的一些题目。比如SASMOG4-2015—Q16,由91个单位正方形,构成边长大于一个单位的长方形,其长和宽分别是多少,同样也用到了分解因数的方法。到了初中,求解一些题也会用到因式分解及因数分解,比如x、y是自然数,已知x+xy+y=32,求x+y的值,这里就用到了因式分解以及分解质因数的方法。
欢迎关注、转发、交流与讨论。期待共同努力,能做一些有助于让孩子们提高学习效率的事情,让他们有更多的时间去锻炼、去思考。


















评论