物理学之美：杨振宁的32项科学贡献

防走失，电梯直达安全岛报人刘亚东A

来源：知识分子作者：施郁
“对称性支配相互作用” 原理的历史脉络是：爱因斯坦—外尔—杨振宁

导 读
✚●
○2021年9月22日，是杨振宁先生农历100岁生日，学术界纷纷推出活动或文集祝贺杨振宁百岁诞辰（据李炳安、邓越凡两位教授考证，杨振宁先生生日为10月1日，恰巧与国庆、杨振宁发表获诺贝尔奖之论文的日子相同，而杨振宁先生护照上的生日为9月22日，故《知识分子》和《赛先生》各取一说）。过去几周，《知识分子》与《赛先生》联合推出了 “百年风华杨振宁” 系列文章。本期推送施郁教授特别撰文，按时间顺序评介杨振宁先生的32项科学贡献，对于这些工作的背景、内容、意义和影响依次作简要介绍和分析，再作进一步的讨论。本文关注各个工作之间的关联，分析杨振宁先生的风格和品味，体现他的科学历程。作者强调，对于物理学之美的追寻贯穿了杨振宁的科学生涯，特别是，杨-米尔斯理论和“对称性支配相互作用”原理大大深化了对于自然定律美与真的关系的认识。本文较早版本收入清华大学的《杨振宁先生百岁华诞文集》。在由清华大学、中国物理学会、香港中文大学主办，于清华大学举行的杨振宁先生学术思想研讨会上，作者作了演讲《物理学的美与真：杨振宁的科学贡献》。视频链接：https://www.koushare.com/video/videodetail/16204目录1. 引言2. 分项评述3. 影响和引用情况4. 眼光、坚持、力量5. 杨-米尔斯理论的后续发展6. 物理定律的定律
撰文 | 施郁（复旦大学物理学系）
● ● ●

引 言

2002年在巴黎举行的国际理论物理大会的最后一个报告中，杨振宁指出， 二十世纪理论物理的主旋律是量子化、对称性和相位因子 [1]。

杨振宁对三个主旋律都有重要贡献。而对称性更是杨振宁本人物理生涯的主旋律，对于物理学之美的追寻贯穿了杨振宁的科学生涯。

1928年， 6岁的杨振宁在海滩捡贝壳，与众不同地挑选极小却精致的 [2]。异于常人的独特的观察力、品味和风格在他成年后的物理学生涯中不断表现出来，成就了一位当代最卓越的理论物理学风格大师和物理学基本理论结构设计师 [1,2,3]，正如弗里曼·戴森（Freeman Dyson）1999年所说 [4]：“杨教授是继爱因斯坦和狄拉克之后，20世纪物理学的卓越风格大师……向费米学到了最多的物理……他是保守的革命者。”

对此，戴森于2015年解读 [5]：“我强调了杨振宁的3个杰出品质，这些品质通常很难结合在一起。第一，奇特的数学技巧，这使得他能够解决技术问题。第二，对自然的深刻理解，这使他问重要的问题。第三，社会精神，这使他在中华文明的复兴中扮演了重要角色。这三个品质共同将他塑造成他，一位继往开来的保守革命者。”

杨振宁很重视物理上的风格和品味 [1,2,3]。对于二十世纪的几位理论物理大师，他用 “深广” 形容爱因斯坦；用 “笛卡尔式的纯粹”（Cartesian purity）形容狄拉克, 称其工作是 “神来之笔” “秋水文章不染尘”，还用高适的诗 “性灵出万象，风格超常伦” 描写狄拉克方程和反粒子理论；又用 “厚实” 和 “稳健有力（Solidity, Strength）” 形容费米；用 “深刻的洞察力”（Deep insight）形容海森堡；用 “威力”（Power）形容泡利。

杨振宁回忆：“我物理上的品味很大程度上形成于1938年到1944年在西南联大学习的时期。这些年里，我开始欣赏爱因斯坦、狄拉克和费米的工作。他们当然有不同的风格。然而他们都有一种能力，能够从物理概念、理论结构或者物理现象提炼出基本，然后集中于本质……我不能与海森堡的风格共振。但是这不是说我不能领会到他是一位伟大的物理学家。我一直能领会到。” [4]

杨振宁本人的风格受到爱因斯坦、狄拉克和费米三种风格的影响，也具有 “提炼出基本，集中于本质” 的能力。

我尝试用4个词来描绘杨振宁的风格：原创、优雅、功力、物理。

1983年杨振宁出版了《论文选集及评论（Selected Papers with Commentaries）》[3]。2013年，杨振宁又出版了续集《论文选集及评论II（Selected Papers II With Commentaries）》[1]。在1983年文集的序言中，杨振宁引用了唐代诗人杜甫（712-770）的名句：

“文章千古事，得失寸心知。”

这句诗总结了杜甫的创作心态，深得杨振宁喜爱，曾经在自己的诗《赞陈氏级》中化用此句：“造化爱几何，四力纤维能。千古寸心事，欧高黎嘉陈。” [2] 陈省身发现纤维丛理论中的陈氏级（Chern Class），贡献极大，十年后杨振宁和米尔斯提出非阿贝尔规范场理论，再二十年后杨振宁和吴大峻意识到规范场和纤维丛的对应。

杜甫的这个诗句也用来反映了杨振宁自己的研究心态。正如他在该书2005年再版序言中所说，这本论文选集是一个人在物理学一个很激动人心的时代中的旅程的记录。事实上，这同时也是20世纪下半叶理论物理被一位关键参与者记下的发展史。

戴森评论 [4]：“所选的文章有的重要，有的不重要。有的是专业的，有的是通俗的。每篇文章都是珍品。弗兰克（杨振宁的非正式英文名字）没有试图将尽量多的硬科学塞进这五百页。他试图在五百页中向我们展示一位伟大科学家的精神。他辉煌地成功了。”

“文章千古事，得失寸心知” 也刻于一个黑色立方体的上平面，那是杨振宁90岁时收到的一件生日礼物。立方体的四个垂直平面则分别刻了他对统计力学、凝聚态物理、粒子物理、场论等物理学四个领域的共13项重要贡献：

（A） 统计力学

A1. 1952 Phase Transition（相变理论）。论文序号：[52a]， [52b]， [52c]。

A2. 1957 Bosons（玻色子多体问题）。论文序号：[57a]，[57b]，[57h]， [57i]， [57q]。

A3. 1967 Yang-Baxter Equation（杨-巴克斯特方程）。论文序号：[67e]。

A4. 1969 Finite Temperature（1维δ函数排斥势中的玻色子在有限温度的严格解）。论文序号：[69a]。

（B） 凝聚态物理

B1. 1961 Flux Quantization（超导体磁通量子化的理论解释）。论文序号：[61c]。

B2. 1962 ODLRO（非对角长程序）。论文序号：[62j]。

（C） 粒子物理

C1. 1956 Parity Nonconservation （弱相互作用中宇称不守恒）。论文序号：[56h]。

C2. 1957 T，C and P （时间反演、电荷共轭和宇称三种分立对称性）。论文序号：[57e]。

C3. 1960 Neutrino Experiment （高能中微子实验的理论探讨）。论文序号：[60d]。

C4. 1964 CP Nonconservation （CP不守恒的唯象框架）。论文序号: [64f]。

（D）场论

D1. 1954 Gauge Theory（杨-米尔斯规范理论）。论文序号：[54b]， [54c]。

D2. 1974 Integral Formalism（规范场的积分形式）。论文序号：[74c]。

D3. 1975 Fibre Bundle（规范场与纤维丛的对应）。论文序号: [75c]。

论文序号是杨振宁给自己所有文章编的序号（出版年加上排序字母）。统计力学与凝聚态物理密切相关，场论与粒子物理密切相关，区分有一定的任意性，只是统计力学和场论的理论性和普遍性更强点，而凝聚态物理和粒子物理更针对具体现象。

参照代表朗道10项重要贡献的 “朗道十诫”，杨振宁的13项重要贡献或可称为 “杨振宁13诫” [6]。

我们再按时间顺序列出杨振宁的19项其他贡献：

E1. 1947 Quantized Spacetime（量子时空）。论文序号：[47a]。

E2. 1948 Angular Distribution（角分布）。论文序号：[48a]。

E3. 1949 Weak Interactions（弱相互作用普适性）。论文序号：[49a]。

E4. 1949 Fermi-Yang Model（费米-杨模型）。论文序号：[49b]。

E5. 1950 Selection Rule（π0选择定则）。论文序号：[50a]。

E6. 1950 Phase Factors of the Parity Operator（宇称算符相位因子）。论文序号：[50c]。

E7. 1956 G Parity（G宇称）。论文序号：[56d]。

E8. 1957 Two-Component Theory of Neutrino（中微子二分量理论）。论文序号：[57f]。

E9. 1957 Hyperon（超子衰变）。论文序号：[57o]。

E10. 1960 Intermediate Boson（中间玻色子）。论文序号：[60e]。

E11. 1962ξlimit（ξ极限）。论文序号：[62i]。

E12. 1967 Nonabelian Wu-Yang Monopole（非阿贝尔吴-杨磁单极）。论文序号：[67d]。

E13. 1968 High Energy Scattering（高能散射几何模型）。论文序号：[68b]，[68c]，[68d]。

E14. 1970 Charge Quantization（电荷量子化）。论文序号：[70a]。

E15. 1976 Monopole Without Strings（无弦磁单极）。论文序号：[76c]，[76d]。

E16. 1977 Self-dual Gauge Fields（自对偶规范场）。论文序号：[77g]。

E17. 1978 SU(2) Monopole in 4D Spherical Space（4维球空间上的SU(2)磁单极）。论文序号：[78a]，[78g]。

E18. 1989 η pairing（η配对）。论文序号：[89d]。

E19. 1990 SO(4) in Hubbard Model（哈伯德模型的SO(4)对称性）。论文序号：[90b]。

下面按时间顺序，对这32项贡献简要评述，其间穿插对杨振宁科学历程的回顾。然后分析这些工作的影响，并作进一步讨论。我们以前对13项重要科学贡献作过评述 [6]，为完整起见，这里融入部分内容。

分项评述

1947 年的量子时空（E1）
1945年杨振宁去美国留学，希望跟随费米做实验论文，或者以量子对称性开创者维格纳（Eugene Wigner）为师，因此进入了费米所在的芝加哥大学。当时费米的实验室不能接受外国人，因此将杨振宁推荐给理论家特勒（Edward Teller）和实验家艾立逊（Sam Allison）。
关于芝加哥时期，杨振宁的老同学、1988年诺贝尔奖得主斯坦伯格（Jack Steinberger）曾经回忆：“最令人印象深刻的是杨振宁，战后，24岁的他从中国来，虽然战时中国条件有限，他来芝加哥读研究生时，熟悉所有的现代物理” [7]。又说 “基本上知道我们所有课程的内容” [8,9]。
1947年年初，杨振宁给黄昆写信，说有点幻灭（disillusioned）[1]。然而就在这一年，他写了E1这篇短文，在Snyder刚发表的理论中，讨论了通过时空弯曲实现时空量子化的平移不变性。这也可归类为对称性方面的工作，是他在美国的第一篇文章。
在美国，杨振宁逐步走到物理学前沿，特别是，二十世纪下半叶是粒子物理蓬勃发展的时代，杨振宁和他的同事与粒子物理一同成长。
1948年的角分布（E2）
如果在杨振宁所有的论文和演讲中找出一个主导性基调，那就是对称性。对称性是物理学之美的一个重要体现，也在粒子物理中扮演重要角色。维格纳指出，基本粒子就是庞加莱群（由洛伦兹变换和时空平移组成）的不可约表示。二战后，物理学家回到基础研究，粒子物理大发展。对称性分析是关键，而这正是杨振宁所擅长，他逐步成长为理论粒子物理的缔造者之一。
杨振宁对粒子物理诸多具体问题的贡献表现出他对对称性分析的擅长。他往往能准确利用对称性，用优雅的方法很快得到结果，并且突出本质和巧妙之处。
群论是关于对称性的数学。1942年，杨振宁在西南联大请吴大猷指导学士论文。吴大猷给了他一篇关于群论在分子光谱学的应用的综述文章 [3]。杨振宁的父亲介绍他从狄克森（Leonard Eugene Dickson）的书《现代代数理论》（Modern Algebraic Theory）中学习群论。在芝加哥大学，特勒就是群论用于原子、分子和核物理的专家，杨振宁向他学到很多物理，包括群论的应用。
1947年杨振宁还钻研了四个课题，其中之一是核物理和粒子物理中的各种角分布 [1]。角分布（E2）论文与之密切相关。这是杨振宁的博士论文工作，基于对转动对称和空间反演对称的分析，得到核反应和核衰变产物的角分布 [3]。其中β衰变的相对论性情形是特勒建议处理的。在特勒建议下，杨振宁以此为博士论文，以特勒为导师，放弃了做实验的尝试。1948年，杨振宁获博士学位，并留校做了一年教员。
1949年的弱相互作用的普适性（E3）
1948年，杨振宁与李政道和罗森布鲁斯（M. Rosenbluth）注意到，缪子衰变、缪子被原子核俘获与β衰变都有相同数量级的作用强度，猜想由同样的中间场（即后来的中间玻色子）传递。这篇半页纸的文章与其他几个组的文章一道，将弱相互作用确定为一种基本相互作用 [3]。
这篇文章是李政道和杨振宁的第一篇合作论文。李政道1946年从西南联大来到芝加哥大学读博士，导师是费米。
1949年的费米-杨模型（E4）
当时普遍认为介子是基本粒子。但是1949年费米和杨振宁问 “介子是基本粒子吗”，探讨了核子和反核子组成π介子的假设。这具有很重要的历史意义，相当于发现原子时问原子是否可分。
杨振宁后来评论：“我们并没有幻想我们的建议与实际一致。事实上，我倾向于将这个工作完全埋藏在笔记本里，不发表。但是费米说，学生解决问题，研究人员提出问题；他觉得我们提出的问题值得发表。我们提出的问题今天（1963年）还没有解决。” [3] 这是戴森2015年所说的杨振宁问重要问题之一例。
斯坦伯格说：“如果将核子换成夸克，现在还是这个图像。” [8,9] 这说明基本物理思想是最重要的。因渐近自由而获得2004年诺贝尔奖的维尔切克（Frank Wilczek）做过跟斯坦伯格精神一致但更详细的评论，指出费米和杨振宁提出的问题富有成果 [9]：
首先，这个模型坚实地以相对论量子场论为框架（那时量子场论还没有被普遍接受为粒子物理的框架）。第二，借助于结合能，由重得多的粒子组成轻的粒子是个解放性概念，夸克和胶子组成介子和核子正是沿着这条思路。第三，费米-杨模型对强作用采用与弱作用费米理论类似的形式，期待了强和弱作用机制的深刻类似，这是标准模型的中心特征，而标准模型正巧建立在杨振宁本人的杨-米尔斯理论基础上。
1950的π0选择定则（E5）
1949年芝加哥大学的一次讨论会上，有人提出π0介子可以衰变为两个光子。第二天，杨振宁便研究出选择定则 [3]。
这一年，杨振宁加入普林斯顿高等研究院，将在这里工作17年。
1950的宇称算符相位因子（E6）
这是杨振宁在普林斯顿的第一个工作，和蒂欧姆诺（J. Tiomno）探讨了β衰变等过程中，自旋1/2粒子的宇称算符的相位因子。次年，在芝加哥的一个会议上，费米专门安排了一段时间来讨论这篇文章 [3]。
角分布（E2）、π0（E5）和宇称算符（E6）这三篇文章初步确立杨振宁在粒子物理对称性分析上的领先。其中π0文章（E5）最为著名。 1952年的相变理论（A1）
统计力学也是杨振宁的主要研究方向之一，而相变是统计力学的一个中心问题。杨振宁的统计力学旅程始于1942年至1944年在西南联合大学的硕士论文，导师是清华大学的王竹溪。
在芝加哥，当时没有教授对相变感兴趣，包括相变理论的先驱梅耶（Joseph Mayor）。杨振宁在主攻粒子物理之余，保持对统计力学的兴趣。他1947年钻研的四个课题之二是昂萨格（Lars Onsager）的二维伊辛模型严格解，但杨振宁当时没能理解它的整体思想。伊辛模型是统计力学里最基本却极重要的模型，但是它在理论物理中的重要性到1960年代才被广泛认识，这里就有杨振宁的贡献。
在普林斯顿，1949年11月，杨振宁从同事路丁格（Joaquin Luttinger）处了解到，考夫曼（Bruria Kaufman）简化了昂萨格的方法。杨振宁开始研究这个问题。1951年1月，他发现可以计算出自发磁化强度 [3]。
1951年秋，李政道也来到这里，后来去了哥伦比亚大学。两人总共合作了三十多篇文章，包括杨振宁13项重要贡献中的4.5项。
1952年，杨振宁单独以及与李政道合作，共发表了三篇有关相变的重要论文。第一篇就是前一年独自完成的2维伊辛模型自发磁化强度论文，得到了1/8这一临界指数。这是杨振宁做过的最长的计算，是一个绝对的壮举。戴森称其为 “雅可比椭圆函数理论的大师式练习” [10]。在杨振宁建议下，张承修计算了长方形格点，与杨振宁计算的正方形格点的临界指数都是1/8。这是临界指数普适性的最早迹象 [3]。
1952年，杨振宁还和李政道合作完成并发表了两篇关于相变的系列论文，将伊辛模型的研究扩展到格气模型，并严格计算出相图。两篇文章同时投稿和发表，发表后引起爱因斯坦的兴趣。论文通过解析延拓到逸度的复平面上，巧妙地研究了巨配分函数的解析性质，它的零点的分布决定了状态方程和相变性质等热力学性质。热力学极限下，零点趋向正实轴，代表相变。这两篇论文澄清了相变本质，消除了梅耶1937年文章之后一直争论不断、对于同一相互作用下可存在不同热力学相的疑惑，即：“气体分子如何‘知道’它们何时聚集成液体还是固体” [6]。
这两篇系列论文的高潮是第二篇论文中的单位圆定理，它指出，对于伊辛模型或者与之等效的吸引相互作用的格气模型，巨配分函数的零点分布于复平面的单位圆上。在统计力学和场论中，这个理论精品就像一个小而精致的贝壳，至今魅力不减。杨振宁本人称其为 “一个小珍品”。数学物理学家吕埃勒（David Ruelle）以此作为杰出典范，解释数学定理是如何被猜测和证明的 [11]。
1954年的杨-米尔斯规范理论（D1）
杨振宁1947年在芝加哥大学钻研的四个课题之三是，泡利的综述文章中介绍的电磁规范理论。杨振宁对于通过规范（指相位）不变性得到电荷守恒印象深刻，后来才知道这个理论是外尔（Hermann Weyl）创立的。1947年杨振宁曾试图将它推广到非阿贝尔规范理论，以便描述粒子间的相互作用，但是没有成功 [1,3]。当时也有实验背景。1947 年，π+介子在宇宙线中被发现。所以杨振宁试图与介子挂钩。
不变性就是对称性。诺特（Emmy Noether）定理指出，对称性对应于守恒量。因此 “对称” 和 “守恒” 这两个词常可以互换。规范不变性是说，在波函数或量子场的相位变换下，物理定律保持不变。相位变换的意思是乘以一个相位因子，这是一个模为1的复数。而且外尔考虑的是局域相位变换，也就是说，相位因子依赖于时空坐标。两个复数相乘，如果顺序颠倒，乘积不变，这叫阿贝尔。非阿贝尔规范理论将单个的复数推广为矩阵。两个矩阵相乘，如果顺序颠倒，乘积可能改变，因此叫做非阿贝尔。规范对称性与通常的对称性有一点不同，它是指对于同一个物理状态有不同描述，是一种冗余，而通常的对称性是指不同状态之间的关系。
1953年至1954年，杨振宁在布鲁克海文实验室访问，与米尔斯（Robert Mills）在同一办公室。杨振宁向米尔斯介绍了推广规范理论的尝试。当时，越来越多的粒子被发现。人们考虑各种形式的相互作用。杨振宁觉得，显然需要一个原理，来写下相互作用 [1,3]。用戴森2015年的话说，杨振宁问了非常重要的问题：如何用规范原理确定相互作用？
1954年，杨-米尔斯规范理论（即非阿贝尔规范理论）发表。在两篇短文中，杨振宁和米尔斯将外尔的阿贝尔规范理论推广到非阿贝尔规范理论。这两篇短文是：
●C. N. Yang, R. Mills, 同位旋守恒与广义规范不变, Phys. Rev. 95, 631 (1954)；● C. N. Yang, R. Mills, 同位旋守恒与同位规范不变, Phys. Rev. 96, 191 (1954)。
这个当时没有被物理学界看重的理论，通过后来许多学者于1960到1970年代引入的自发对称破缺与渐进自由的观念，发展成今天的标准模型。其中，电弱统一理论是U(1)XSU(2)杨-米尔斯理论，量子色动力学是SU(3)杨-米尔斯理论。这被普遍认为是20世纪后半叶粒子物理学和量子场论的总成就，主导了长期以来粒子物理学和量子场论的研究。
杨振宁和米尔斯进行这个推广的第一个动机清晰表达于他们1954年的第一篇短文 [3]。那是杨振宁在当年在华盛顿召开的美国物理学会四月会议M会场（主持人是戴森）所作报告的摘要，大概在4月1日之前投稿。标题是 “同位旋守恒与广义规范不变”，摘要写道：“电荷是电磁场的源。这里的一个重要概念是规范不变性，它紧密相关于(1)电磁场的运动方程，(2)流密度的存在，(3)可能存在的带电的场与电磁场的相互作用。我们尝试将这一规范不变性的概念推广，以用于同位旋守恒。”
因此，杨振宁和米尔斯所做的是将同位旋守恒类比于电荷守恒：既然电荷守恒是阿贝尔规范不变性的后果，那么同位旋守恒也是一种规范不变性的后果，因此将电磁相互作用与阿贝尔规范场之间的紧密关系推广到一种新的相互作用与非阿贝尔规范场之间的紧密关系。电磁相互作用定律和同位旋守恒都是有实验基础的。
另一个动机，正如第二篇短文（论文）的标题和摘要强调的，是将同位旋对称从与时空无关的整体对称性推广到依赖于时空的局域对称性，从而确定相互作用的形式 [3]。标题是 “同位旋守恒与同位规范不变”，摘要写道：“……探讨了在局域同位旋转动下的不变性。这导致建立同位旋规范不变性原理，以及b场的存在，它和同位旋的关系同于电磁场与电荷的关系。b场满足非线性微分方程。b场的量子是自旋1、同位旋1、电荷±e或零的粒子。”
所以杨振宁和米尔斯的思路如下。与局域相位变换联系的阿贝尔规范不变性表现为电荷守恒，并导致电磁相互作用。外尔发现了这个理论结构，虽然当时电磁相互作用已经是已知的。杨-米尔斯理论将它推广为与局域同位旋变换联系的非阿贝尔规范不变性，由此决定新的、待确定的相互作用。
从数学观点讲，这是从描述电磁学的阿贝尔规范理论到非阿贝尔规范理论的推广。而从物理观点讲，是用此种推广发展出新的相互作用的基础规则。也就是说，他们敲开了后来杨振宁所说的 “对称支配力量”（或者说 “对称性支配相互作用”）这一原理的大门。这是划时代的，革命性的。
今天知道，在主宰世界的4种基本相互作用中，引力由爱因斯坦的广义相对论描述，电磁和弱相互作用统一成电弱相互作用，它和强相互作用都分别由杨-米尔斯理论描述，而描述引力的爱因斯坦的广义相对论也与杨-米尔斯理论有类似之处。杨振宁称此为 “对称支配力量”（或 “对称性支配相互作用”）[3]。这是最初由爱因斯坦在创立广义相对论时开启的原理。杨-米尔斯理论是二十世纪后半叶伟大的物理成就，杨-米尔斯方程与麦克斯韦方程和爱因斯坦方程共同具有极其重要的历史地位。
杨-米尔斯理论的成功是物理学史上的一场革命。但是杨振宁的出发点并不是要搞革命，而是要在复杂的物理现象背后寻找一个原理，建立一个秩序。这种秩序的建立是杨振宁追求物理美的一个主要表现。作为保守的革命者，他引起的革命是不得已而为之，是建设性的，而非破坏性的。但当革命性的思想确实需要时，他又果断地采纳。虽然最初得到杨-米尔斯规范理论时，杨-米尔斯规范粒子的质量问题不能解决，但物理直觉、理论的美以及对规范对称性的重视使得杨振宁相信这个理论一定是正确的一步。
1956年的G宇称（E7）
1955年，反质子发现后，杨振宁和李政道提出G 宇称的概念，联合电荷共轭对称和同位旋对称，由此确定了强相互作用过程的一些选择定则 [3]。
1956年的弱相互作用中宇称不守恒（C1）
1956年，θ-τ之谜是物理学中最重要的难题。θ和τ这两个粒子在弱相互作用主宰下，分别衰变成2个和3个π介子，而π介子的宇称是-1，因此θ和τ的宇称分别是+1和-1。但是θ和τ的质量和寿命完全一样。当时普遍讨论，在θ和τ的衰变中，由于某种特殊原因，宇称是否可以不守恒。如果宇称守恒，那么θ和τ就是两个不一样的粒子，大自然就需要将它们的质量和寿命微调成完全一样。这是很奇怪的，很不自然，不美。
杨振宁和李政道从θ-τ之谜这个具体的物理问题走到一个更普遍的问题，将这个难题扩展为弱相互作用的普遍问题，又提出 “宇称在强相互作用与电磁相互作用中守恒，但在弱相互作用中也许不守恒” 的可能，将弱相互作用主宰的衰变过程独立出来，然后经具体计算，发现，原来以前并没有实验证明在弱相互作用中宇称是否守恒，他们还指出了好几类弱相互作用关键性实验，以测试弱相互作用中宇称是否守恒。
β衰变实验家吴健雄于1956年夏，决定做他们指出的几类实验中的一项关于极化钴60原子核（60Co）β衰变的实验（杨振宁后来评论她 “独具慧眼”）。吴健雄邀请低温物理学家安布勒（E. Ambler）、海沃德（R. W. Hayward）、霍布斯（D. D. Hoppes）和胡德森（R. P. Hudson）进行合作。次年1月初，她领导的实验表明，在弱相互作用中，宇称确实不守恒，引起整个物理学界的巨大震荡。因为 “对于宇称定律的透彻分析，导致关于基本粒子的重要发现”（诺贝尔奖颁奖词），杨振宁和李政道获得1957年的诺贝尔物理学奖。
回顾历史，从经典物理以及晶体结构，到量子力学与粒子物理，对称性分析是物理学中的有力工具。而量子力学的兴起使得对称性在物理学中占据前所未有的重要地位。它将原子光谱中的量子数l和m解释为转动算符的本征值。到了1950年代，所有的量子数与对称操作联系在一起。宇称与空间反演或镜面反射相联系。因此，宇称守恒有着直觉上的吸引力，被当作自然的、神圣的，而且在实验上非常有用，特别是在核物理的实验分析方面。所以不难理解，在这样的气氛下，1956年杨振宁和李政道建议检验弱相互作用中宇称是否守恒的文章受到普遍的异议乃至嘲弄。同样也不难理解，1957年初实验结果宣布后，杨振宁和李政道的这一工作当年即被嘉以诺贝尔奖。这个得奖速度创造了诺贝尔奖整个历史上的记录，至今未被打破，前无古人，后无来者。
温伯格（Steven Weinberg）说过：“李政道和杨振宁扭转了从爱因斯坦开始的物理学家的一个倾向，即对称性是不言而喻的原理。每个人都感到这一突破带来的激动。” [12]
1957年的时间反演、电荷共轭和宇称三种分立对称性（C2）
质疑弱相互作用中宇称是否守恒的论文预印本引起欧米（Reinhard Oehme）于1956年8月致信杨振宁，提出弱相互作用中宇称（P）、电荷共轭（C）、时间反演（T）三个分立对称性之间的关系的问题。这导致杨振宁、李政道和欧米讨论P、C、T各自不守恒之间的关系 [3]。他们1956年接近年底时写好论文，宇称不守恒实验上确定后， 1957年1月7日投稿。此文对1964年所有的关于CP不守恒的理论分析有决定性的影响。
物理定律在某个层面的不对称在实验揭示出来后，可以用更全面的对称来 “挽救”。所以当时人们期待C和P的联合操作CP下的对称性。杨振宁1983年评述 [3]：“为什么我们没有预料到CP违反？原因又是，每个人自然偏向于更多的对称性。在这个情形下，事实上，也没有疑难驱使我们考虑CP违反。1964年以前的所有的工作都是将电荷共轭包括进来，重新定义反射操作。” 现在依然认为CPT联合操作是守恒的。
1957年的中微子二分量理论（E8）
3天以后，1月10日，杨振宁和李政道又将中微子二分量理论投稿。宇称不守恒意味着，可以用手征性区分中微子和反中微子（自旋总是沿着或逆着运动方向），各自的波函数只有两个分量。文章详尽讨论了实验相关问题，简洁地指出中微子探测的截面应该是原来理论结果的双倍 [3]。在有实验证据之前不随便猜测，而有实验证据后透彻讨论，这种研究风格有费米之风。
1960年，中微子发现者雷纳斯（Frederick Reines）和科万（Clyde Cowan）宣布，截面确实应该比他们最初（1956年）公布的增加一倍 [13]。1979年雷纳斯解释：“当初对于探测器效率估计过大” [14]，在2002年诺贝尔演讲中，雷纳斯再次重申 “正如我们几年后从李政道和杨振宁处了解到的，截面应该扩大到两倍，因为宇称不守恒及中微子手征性。
1957年的玻色子多体问题（A2）
起源于对液氦超流的兴趣，杨振宁在1957年左右与合作者完成了一系列关于稀薄硬球玻色子多体系统的论文。这是物理上受液氦超流驱动、数学上定义完善的模型。
1955年开始，杨振宁和黄克孙、路丁格合作，将赝势法（最初由费米等人在核物理中发展出来）用到玻色子多体问题。由于一个发散问题，这个工作的两篇论文迟至1956年10月才投稿[3]。
1956年4至6月，杨振宁和李政道集中研究θ-τ之谜。在写好相关论文、等待宇称实验结果的那段时间，杨振宁和李政道研究玻色子多体问题，用二元碰撞方法，得到了与赝势法一致的结果，而且通过将最发散的项求和，首先得到了正确的基态能量修正。随后，又和黄克孙用赝势法得到同样的结果以及低激发谱。他们得到的能量修正中最令人惊讶的是著名的平方根修正项，被称为 “李-黄-杨修正”。但当时无法得到实验验证。
由于粒子物理方面的工作压力，他们写了二元碰撞计算的简单总结，12月投稿。1957年1月，在多体理论会议上，杨振宁对这两个方法作了综述。3月19日，他们将赝势法的结果投稿。
在获得诺贝尔奖之后，杨振宁和李政道有时间回到玻色气体问题。他们先是将李-黄-杨赝势法扩展到有限温度，写了两篇文章，然后又写了5篇文章，通过巨正则系综和变分方法讨论了各种性质 [3]。1960年，在多粒子问题会议上，杨振宁对这些工作做了综述，其中有一些讨论与两年后的非对角长程序论文相关。
出乎他们的预料，近年来，他们的理论结果，特别是 “李-黄-杨修正”，随着冷原子物理学的发展而得到了实验证实。1992年，杨振宁被问到，如何 “选择10到20年后变得重要的问题”，他回答：“必须寻找与物理现象或者与物理学基本结构直接相关的课题。” [2] 玻色子问题就是他这一方法论的一个很好的例子，而且是40-50年后特别重要。
1957年的超子衰变（E9）
宇称不守恒确立后，人们纷纷研究其他弱衰变实验，包括超子衰变为π介子和核子。杨振宁和李政道对此作了分析。他们定义的几个关键参数成为这个领域的标准语言。
1960年的高能中微子实验的理论探讨（C3）
1960年，实验物理学家施瓦兹（Melvin Schwartz）指出如何通过中微子束得到更多弱相互作用的实验信息。李政道和杨振宁在理论上探讨了高能中微子实验的重要性 [3]。这是关于中微子实验的第一个理论分析，引导出后来许多重要研究工作。
斯坦伯格与莱德曼（Leon Lederman）及施瓦兹因为中微子束方法和μ中微子的发现而共同获得1988年诺贝尔物理学奖。斯坦伯格指出：“这种实验的物理意义在李政道和杨振宁的论文中被列表讨论，这个文章被证明是预知未来的……当中微子束和探测器越来越有力后,这些过程成为多年深入实验的课题。” [9]
在这篇文章中，杨振宁和李政道也讨论了传递弱相互作用的中间玻色子，并命名为后来被广泛采用的W±。
1960年的中间玻色子（E10）
1957年4月的罗切斯特会议上，杨振宁曾经评论 [3]：“如果β衰变相互作用是矢量相互作用而不是标量相互作用，人们应问一个问题，这是否与一些矢量场有关。而这些矢量场产生于局域守恒定律的概念。”这是历史上第一次提出弱相互作用的中间矢量场可能是规范场。后来有更多人这么猜测。
但是杨振宁和李政道并不喜欢猜测性的工作，而是采取更踏实的策略，集中于中间玻色子的唯象和逻辑分析 [3]。他们考虑实验事实的限制，对中间玻色子场作了若干理论探讨。他们另外还与合作者马克斯坦（P. Markstein）作了中微子束产生W粒子的截面计算。
1961年的超导体磁通量子化的理论解释（B1）
1961年夏，杨振宁访问斯坦福大学 [3]。在那里，费尔班克（William Fairbank）和戴佛（Bascom Deaver）在实验上发现超导环中磁通量以hc/2e为单位的量子化。费尔班克疑惑，这是不是因为电磁场有超越麦克斯韦理论的新规律。杨振宁和伯厄斯（Nina Byers）给出了这一现象的理论解释，证明电子配对即可导致观测到的现象，而无需引入新的关于电磁场的基本原理，并纠正了伦敦（Fritz London）和昂萨格的推理错误。证明过程中，他们将规范变换技巧运用于凝聚态系统中。这也是杨振宁与实验家互动的一个例子。
1962年的ξ极限（E11）
这篇文章也是杨振宁和李政道关于W粒子的唯象和逻辑研究，是关于它们与电磁场的相互作用。为了处理一个发散问题，杨振宁发明了叫做ξ极限的方法 [3]。这个方法后来也被用在规范理论中。
这篇文章是两人最后一篇合作论文。1999年诺贝尔奖得主韦尔特曼（Martinus Veltman）说 [15]：“他们刚开始系统研究矢量玻色子（弱相互作用的W和Z），无法知道他们在发展标准模型上可以走多远。”
1962年的非对角长程序（B2）
杨振宁的玻色气工作引导他考虑密度矩阵的结构，磁通量子化工作引导他考虑超导理论的涵义，这些问题最终统一起来。1962年，杨振宁提出非对角长程序的概念，统一刻画超流和超导（或称量子凝聚）的本质，同时也深入探讨了磁通量子化的根源。这是当代凝聚态物理的一个关键概念。杨振宁后来指出，此文是 “我一直所喜爱的文章，虽然意犹未尽。” [3]
2006年，因为氦3超流的理论工作而分享2003年诺贝尔物理学奖的莱格特（Anthony Leggett）出版了一本关于各种量子凝聚的专著，该书的序言包含以下说明：“我从一开始就采纳由杨振宁首先阐明的观点，即应该简单地考虑在对所有粒子的行为平均之下单粒子或者粒子对的行为，用术语说，就是单粒子或两粒子密度矩阵。” [16]
1964年的CP不守恒的唯象框架（C4）
1964年，克里斯滕森（James Christenson）、克罗宁（James Cronin）、菲奇（Val Fitch）和特莱（René Turlay）的实验发现了弱相互作用中CP不守恒。后来克罗宁和菲奇因此获得1980年的诺贝尔物理学奖。
1957年宇称（P）不守恒发现后，人们猜测CP守恒，没有想到CP也不守恒。1964年CP不守恒的实验发现引发了很多理论文章。其中有众多乱猜其根源的理论文章。杨振宁和吴大峻没有理会那些脱离实际的理论猜测，而作了CP不守恒的唯象分析，集中于未来实验的仔细分析，建立了后来分析此类现象的唯象框架。这反映了杨振宁脚踏实地的作风，显示出费米的影响。
克罗宁1993年指出：“在1964年的所有这些理论文章中，只有两篇今天还被引用。其中之一是吴大峻和杨振宁的题为‘K介子衰变的CP守恒的破坏的唯象分析’的文章……在过去的29年中是实验的指导。” [10]
与三种分立对称性（C2）论文一道，此文定义了使用至今的理论框架和术语。斯坦伯格回忆，正是吴-杨文章启发他去测量中性K介子衰变的主要参数 [9]。
1967年的非阿贝尔吴-杨磁单极（E12）
杨振宁认为不应当马虎地将规范场变成唯象的东西，因为牵强尝试破坏了规范不变性 [3]。因此1955年到1967年之间，虽然杨振宁时不时回到规范场问题，但是没有就此发表任何论文。
1960年代后期，杨振宁重返规范场。本文是他1955年之后的第一篇规范场论文，是和吴大峻获得的经典纯杨-米尔斯理论的第一个解。他们的策略是先寻找无奇点的解，再通过微扰寻找激发。这个方案与对称破缺的思想有类似 [3]。
1967年的杨-巴克斯特方程（A3）
1947年在芝加哥大学，杨振宁钻研的四个课题之四是贝特（Hans Bethe）1931年关于1维铁磁体的波函数的一个假定，关键是自旋波没有衍射。1951年，杨振宁研究2维伊辛模型时，又仔细钻研了贝特的方法。
1962年，杨振宁完成非对角长程序工作之后，寻找具有这种长程序的模型。这个寻找将他引导到量子统计模型的严格解，并重燃他对贝特假定的兴趣。他研读了利布（E. H. Lieb）和林内格（W. Liniger）用贝特假定研究1维δ函数排斥势中玻色子的工作。
1964年至1966年，他和杨振平研究格气模型里的相变及其量子推广。然后研究与之等效的各向异性海森堡链，用了贝特假定，并如此命名，就此发表了一系列论文 [3]。在此期间，杨振宁离开普林斯顿，加入纽约州立大学石溪分校，创办了一所理论物理研究所。
1967年，杨振宁发现1维δ函数排斥势中的费米子量子多体问题可以转化为一个矩阵方程。这个方程后来被称为杨-巴克斯特方程，因为1972年巴克斯特（Rodney Baxter）在另一个问题中也发现这个方程。同一年，杨振宁还写了一篇于次年发表的文章，进一步探讨了此问题的S矩阵。后来人们研究了很多可解模型的S矩阵。
后来人们发现杨-巴克斯特方程在数学和物理中都是极重要的方程，与扭结理论、辫子群、霍普夫代数乃至弦理论都有密切的关系，因而它成为一个重要领域。
另一方面，杨振宁当年讨论的1维费米子问题近年来在冷原子的实验研究中显得非常重要，提供了分析许多1维实验的基础。而他在文中发明的嵌套贝特假设方法次年被利布和伍法岳用来解出了1维哈伯德（Hubbard）模型。
1968年的高能散射几何模型（E13）
1965年开始，杨振宁与合作者（吴大峻、伯厄斯、邹祖德、Benecke、阎爱德等）对高能强子碰撞作了一系列研究，将强子看成一个延展物，发展了一个唯象几何模型，解释了很多现象，提出许多被普遍使用的概念[3]。我们选择1968年与邹祖德合作的这篇文章作为代表。
1969年的一维δ函数排斥势中的玻色子在有限温度的严格解（A4）
1969年，杨振宁和杨振平将1维δ函数排斥势中的玻色子问题推进到有限温度。这是历史上首次得到的有相互作用的量子统计模型在有限温度（T>0）的严格解。近年来，这个模型及其结果也在冷原子系统中得到实验实现和验证。
1970年的电荷量子化（E14）
杨振宁1970年写过一篇1页的文章，证明了规范群的紧致导致了所有的电荷必须是某个基本单位的整数倍。这篇文章很特别，短而深刻。因为拓扑相变和拓扑物质相而获得2016年诺贝尔奖的索利斯（David Thouless）在他的《非相对论物理中的拓扑量子数》（Topological Quantum Numbers in Nonrelativistic Physics）一书中介绍了杨振宁的这个论证。
杨振宁没有研究过生物物理，不过问过一个重要问题。1971年杨振宁给著名的20卷丛书《相变与临界现象》（Domb和Green编，1971-2001）的第一卷写序，最后一段提到统计力学与脑功能的关系 [3]： “今后几十年的一个重大智力挑战是脑组织的问题。记忆存储的基本机制是什么？什么过程实现体内基本上化学的过程与大脑的很特定、非统计的操作之间的联系？最重要的，人脑如何实现概念的形成？我疑惑，是不是这些研究中的物理学精神与感动‘热力学的合理基础’奠基者的并不相似。”
在这个方向上，Little的文章发表于1974年，Hopfield的文章发表于1982年。
1974年的规范场积分形式（D2）
杨-米尔斯理论还把物理与数学的关系推进到一个新的水准。1967到1968年，杨振宁注意到规范场场强与黎曼几何中的黎曼张量之间的类似，意识到规范场有深刻的几何意义 [3]。于是他致力于研究规范场的积分形式，发现了不可积相位因子的重要性，1974年成文发表。
此文在1954年推广规范理论的两个动机之后，给出了第三个动机或者方法：将不可积相位因子推广为不可积李群元素。
1975年的规范场—纤维丛对应（D3）
1970年代早期，杨振宁认识到规范场的几何意义，也意识到规范场的积分形式实际上是一个几何的发展。因此他向赛蒙斯（James Simons）学习纤维丛理论 [3]。
1975年，杨振宁和吴大峻最终意识到物理学家所谓的规范对应于数学家所谓的主坐标丛，而物理学家所谓的势对应于数学家所谓的主纤维丛上的联络，规范场具有整体的几何涵义，可以自然地用纤维丛概念表述。
他们发表了论文《不可积相位因子的概念与规范场的整体形式》（D3），用不可积相位因子的概念给出了电磁学以及杨-米尔斯理论的整体描述，讨论了阿哈罗诺夫-玻姆（Aharonov-Bohm，简称AB）效应和磁单极问题，揭示了规范场在几何上对应于纤维丛上的联络。
这篇文章里面有一个 “字典”，把物理学中规范场论的基本概念准确地 “翻译” 成数学中纤维丛理论的基本概念，包括一个与规范场论中的源相对应的问号，代表当时数学上还没研究。这个字典引起数学界的广泛兴趣，大大促进了数学与物理学以后几十年的成功合作。
这篇文章还包含了用不可积相位因子的概念重新研究狄拉克磁单极。用两个有重叠的区域组成磁单极外的空间，每个区域有矢量势，在重叠区域，两个矢量势只能相差一个梯度，因为磁场强度是唯一确定的。由此得到两个波函数之间的关系。而波函数的单值性就给出狄拉克量子化条件。这解决了有几十年历史的奇异弦困难，揭示了拓扑和物理的深刻联系。文献中有时将其称作阿贝尔吴-杨磁单极。
出于对AB效应的浓厚兴趣和深刻理解，杨振宁还建议外村彰用超导环验证AB效应，实验1986年成功，通过电子全息术测量了AB相位 [1]。
1976年的无弦磁单极（E15）
杨振宁和吴大峻进一步用纤维丛的概念讨论狄拉克磁单极问题，揭示狄拉克磁单极背后的非平庸丛的真正特性。杨振宁认为这是他最优雅的工作之一，发表了两篇文章 [3]。
第一篇文章指出，不可积相位因子文章里面提出的两个有重叠的区域的波函数就是数学上的截面，这个方法消除了奇异弦。然后详细计算分析了角动量算符的本征截面，由磁单极球谐函数（比通常的球谐函数多一个刻画截面的量子数）描写。
第二篇文章给出一个多值的经典拉格朗日量。不需要奇异弦，解释了狄拉克关于经典作用量的结论，即可以加减4πeg/c，导致狄拉克量子化条件。
1977年的自对偶杨-米尔斯场（E16）
对于无源规范场，杨振宁讨论了SU(2)规范场（即杨-米尔斯场）的自对偶条件，得到一个类似拉普拉斯方程的方程。这后来被称为杨方程，被证明是4维可积系统，并被发现与杨-巴克斯特方程有关。自对偶解，即瞬子解，于1975年由Belavin，Polyakov，Schwarz，Tyupkin（BPST）首先得到。
1978年的4维球空间上的SU(2)磁单极（E17）
1978年，杨振宁将狄拉克磁单极推广到5维平直空间或者4维球空间的SU(2)规范场，它具有SO(5)对称性。这是4维平直空间的BPST瞬子解在4维球空间的共形映射。同年他还进一步计算了它的磁单极球谐函数 [8,9]。
1989年的η配对（E18）
杨振宁1960年代就开始寻找本征态具有非对角长程序的费米子模型。1986年高温超导发现以后，2维哈伯德模型成为这个领域的一个重要模型。1989年，杨振宁终于通过η配对机制，在哈伯德模型里找到很多具有非对角长程序的本征态。η配对是总波数为π的电子之间配对（传统配对的总波数为0）。
1990年的哈伯德模型的SO(4)对称性（E19）
在η配对基础上，杨振宁和张首晟很快发现了哈伯德模型的SO(4)对称性，由与η配对相关的SU(2)对称性以及自旋SU(2)对称性构成，因此与超导性和磁性都相关。在此基础上，张首晟发现一个集体模，后来又发展出高温超导的SO(5)理论，将超导性与磁性统一起来。张首晟称之为 “对称性支配相图” [4]。

影响和引用情况

从影响力和引用情况上说，以上列出的32项工作主要可以分为八类。为有助于分析，我们参考 了Web of Science 数据库（截至2021年8月12日。此数据库范围有限，也存在收录遗漏，特别是早期数据。仅作参考）。
第一类是特殊型，属于此类的是杨-米尔斯理论（D1）。 原文已发表多年，成为标准知识，绝大多数研究不再引用原文，反衬其重要性，就好比关于相对论的文章一般不引用爱因斯坦的原文。在Web of Science文章主题中搜索 “Yang Mills” 得到20931篇文章，是原文引用数的十几倍，在标题中搜索 “Yang Mills”，得到6016篇文章；在文章主题和标题中搜索 “non abelian gauge”（非阿贝尔规范），分别得到7224篇和959篇文章；在文章主题和标题中搜索 “nonabelian gauge”，分别得到5290篇和137篇文章。
很少有人知道第一篇短文（会议报告摘要）的存在。第二篇论文被1992篇文章引用（图1）。在1979年的最高峰之前，每年引用呈增加趋势，特别是1960年代初和1970年代中期有跳跃式增加，然后原文引用下降，1990年代以来又持续稳定增加。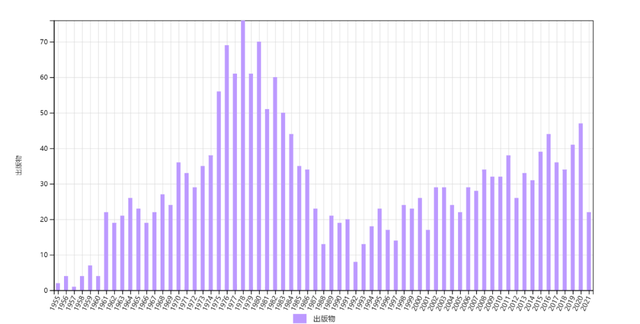
图1 1954年杨-米尔斯理论论文的历年施引文章数，总数为1992。

第二类是不断上升型。属于此类的是相变理论（A1）。其重要性没有在刚发表时立即充分显示，但是此后不断彰显，每年引用数基本保持上升趋势，涨落很小，直到现在。图2显示，三篇文章被引情况非常类似，在1960年代有一个跳跃，然后一直保持增长。通常而言，论文发表若干年后，被引用数开始呈下降趋势。这个 “反常” 的共同形态反映了统计力学的发展情况和持续性，以及这三篇相变论文的重要地位。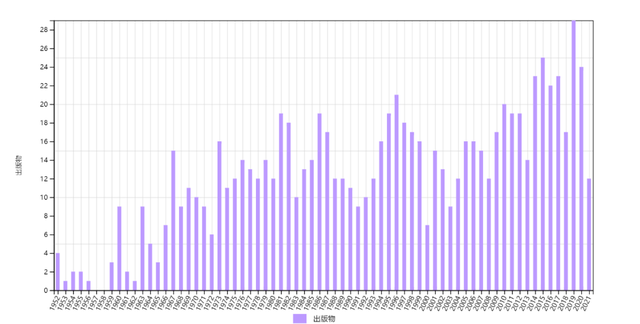
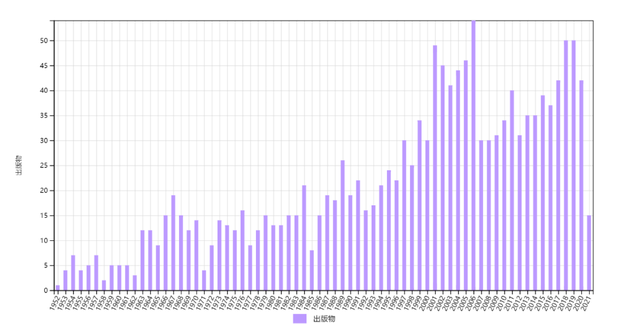
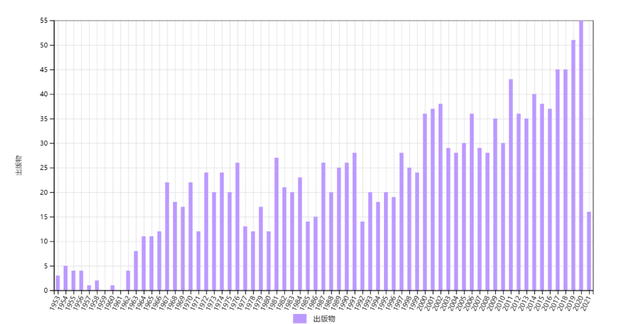图2 1952年三篇相变论文（按发表顺序排列）的历年施引文章数，总数分别是875、1503和1535。
第三类是波浪上升型。属于此类的有杨-巴克斯特方程（A3）和有限温度（A4）（图3）。A3被1775篇文章引用， 1980年代有一个峰，1990年代有一个更大的峰，2000年以来稳定增长。A4被 1052篇文章引用， 在1970年代、1980年代、1990年代以及本世纪，都有越来越高的峰值。
与第二类相比，第三类的引用存在一些明显的下降阶段，但是不改变其向上的长期趋势。这说明该领域在冷却一些时段后有新发展，而且当热潮再次兴起，其持续时间和高度都超过以往。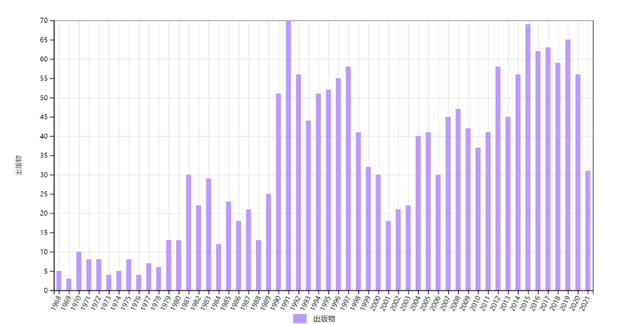
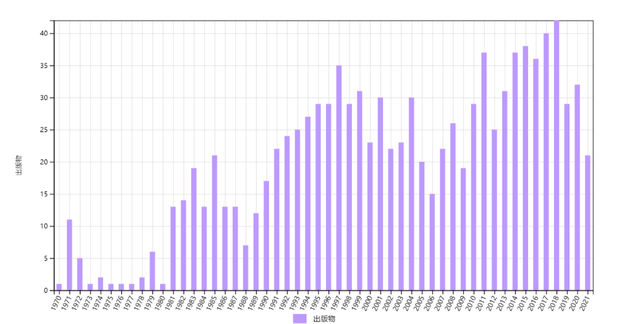图3 1967年杨-巴克斯特方程论文（A3）和1969年有限温度下一维玻色子论文（A4）的历年施引文章数，总引用数分别为1775和1052次。

第四类是衰减复兴型。属于此类的有：宇称（C1），TCP（C2），玻色子（A2），磁通量子化（B1），非对角长程序（B2），角分布（E2），费米-杨模型（E4），π0选择定则（E5），超子衰变（E9）。这类工作发表后立即有其他研究者跟随，体现于发表后紧随的引用峰。然后有个衰减阶段。但是后来因为新的发展，引用又开始增加。
获诺贝尔奖的C1很快为实验所证实，引用出现极高峰（图4）。这是历史里程碑式的工作，问题解决后，成为本领域的核心知识，原文的引用自然出现衰减。但是1990年代以来，引用又增加起来，C2亦类似，不过都没有超过当初的高峰。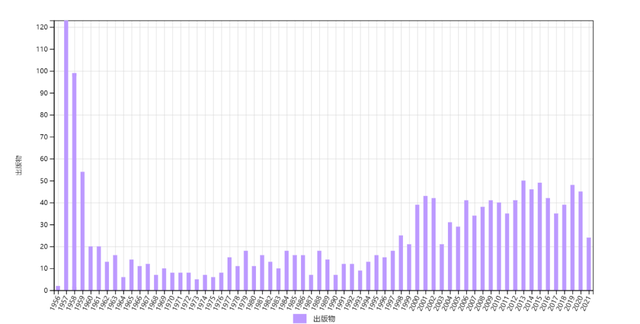
图4 质疑弱相互作用中宇称是否守恒的论文（C1）的历年施引文章数，总数为1640。

而A2、B1、B2复兴后的影响和引用都远超当初，因为后来的相关实验和理论工作远多于当初，理论也越发显得重要。例如，A2研究的玻色气在当初没有完全对应的实验，后来冷原子新领域带来大量后续研究。四篇文章都是这种类型，特别是李-黄-杨修正文章，近年来增长势头强劲，并不断创造新高（图5）。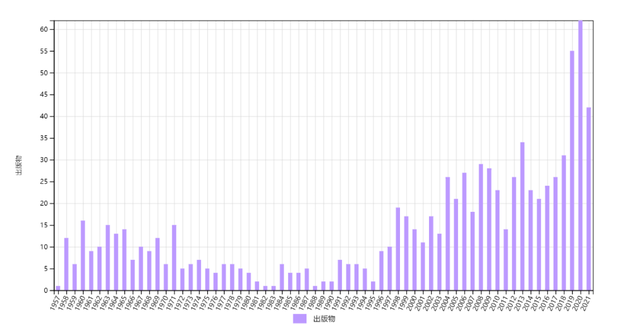
图5 李-黄-杨修正论文（A2）的历年施引文章数，引用总数为897。

磁通量子化（B1）论文发表不久后有个被引高峰，而在1990年代有个大得多的峰，从此保持高原状态，表明很多年后这个领域取得了很大进展。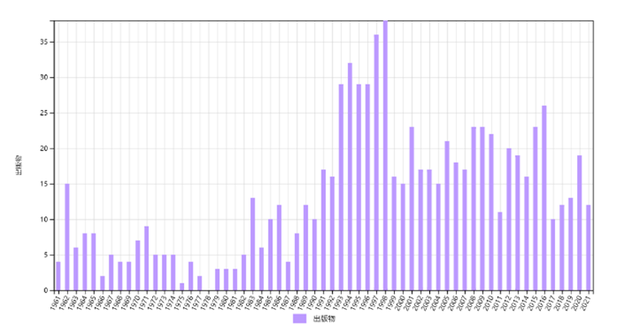
图6 伯厄斯与杨振宁1961年的超导体磁通量子化论文（B1）的历年施引文章数，总数为817。
非对角长程序（B2）论文在1968年左右有一个引用峰值，1980年代后出现了高原（图7），表明近年来关于量子凝聚现象的研究很多。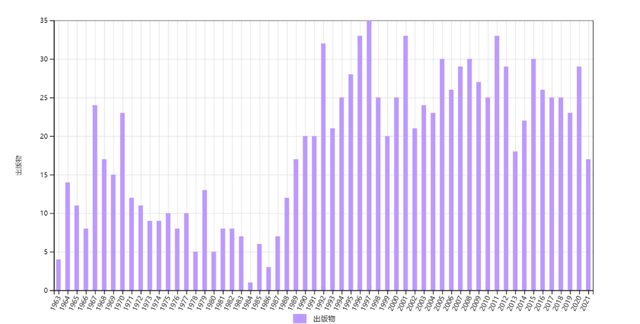
图7 非对角长程序（B2）论文的历年施引文章数，总数为1106。

π0选择定则（E5）的引用复兴尤为突出（图8）。在1950年代引用较多，这是很自然的。有趣的是，从1970年代开始，引用呈现递增趋势。本世纪以来，每年都有很多引用，甚至远超以前，出现了引用高原。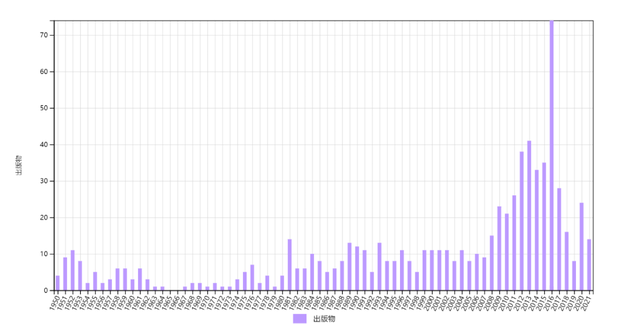
图8 π0介子衰变为两个光子的选择定则文章的历年施引文章数，总数为749。

第五类是恒强型。属于此类的有：规范场—纤维丛对应（D3），无弦磁单极（E15）。
D3和E15的第一篇文章发表后立即产生重大影响，引发热潮。很多年来引用趋势基本没有衰减（图8）。这是因为这些工作发现了丰富的矿藏，物理学家和数学家能从中不断挖掘出新结果。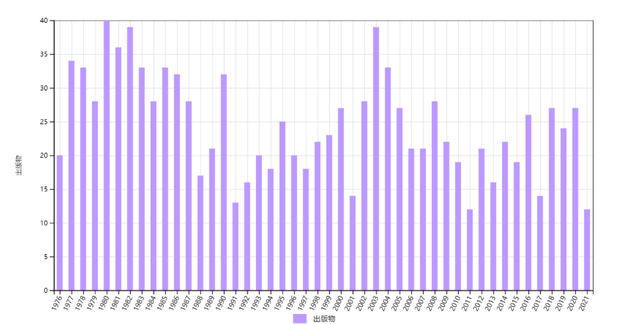
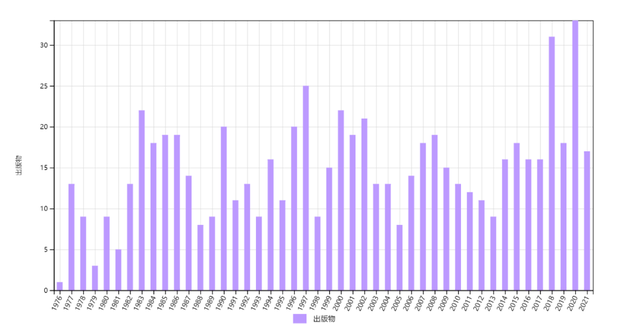图9 杨振宁和吴大峻1975年规范场—纤维丛对应论文（D3）以及1976年第一篇无弦磁单极论文（E15）的历年施引文章数，总数分别为1128和683。
第六类是波浪型。属于此类的有：η配对（E19）。随着相关领域的情况变化，引用数有峰有谷。E19在1997年达到高峰（图10），然后下降，目前正在攀登第二个峰。相对而言，此文发表时间距今还不长。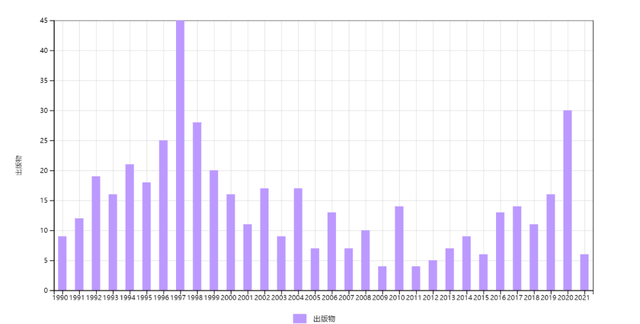
图10 杨振宁1990年关于哈伯德模型中η配对的文章的历年施引文章数，总数为459。

第七类叫沉睡苏醒型。属于此类的有：量子化时空（E1），SU(2)磁单极（E17）。发表后一直引用极少，但是在多年后，年引用数开始逐年增加。从沉睡时间和苏醒幅度来说，最突出的是E1。1990年代之前，引用很少。但是1990年代开始，特别是本世纪以来，因为非对易几何的兴起，引用大大增多（图11）。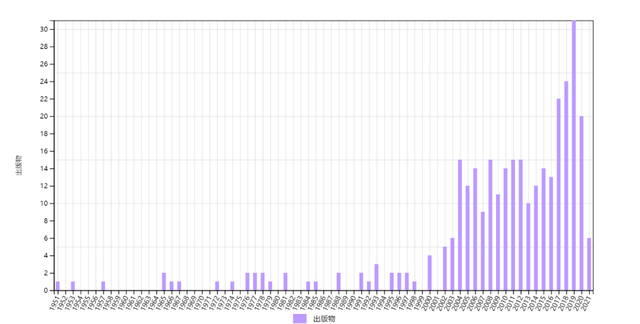
图11 杨振宁1947年量子化时空的短文（E1）的历年施引文章数，总数为322。

第八类是衰减型。属于此类的有：C3，C4，D2，E6，E7，E8，E10，E11，E13，E16。D2和E16属于开辟新领域，其他则都是粒子物理唯象工作，与实验密切联系，有很强的时效性。大多数工作已经成为重要的标准知识，进入教科书，很多人不再引用原文。
E3 和E14引用较少，因为讨论基本问题，很快成为标准知识。E12发表在特勒60岁祝寿文集，很多人不引用原文，而E19发表于一个新杂志，作为支持。二者在Web of Science均没有引用信息，但在Google Scholar分别有80和近千个引用。显然哈伯德模型的SO(4)对称性（E19）影响极大。
迄今为止，13项重要贡献总共被14766篇文章引用17364次，19项其他贡献中的17项（除E12和E19）被 5863篇文章引用 6356次，198篇文章（几乎所有被Web of Science收录的文章）总共被24539篇文章引用32103次。图12显示了历年引用数。可以看到，13项重要贡献和所有文章的总引用趋势非常一致，说明确实是突出代表。更可以看到，杨振宁很多研究成果具有强大的生命力，说明他眼光非常深远。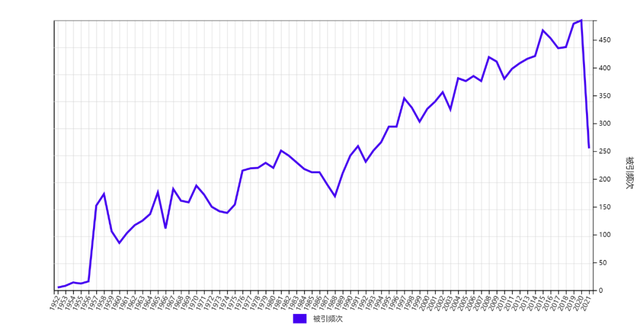
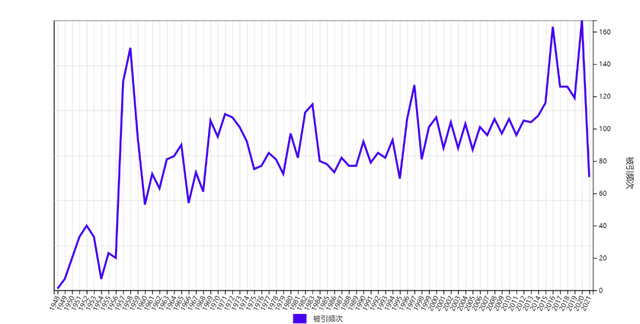
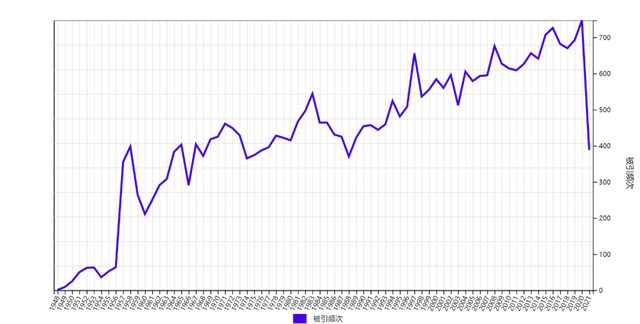图12 杨振宁的13项重要贡献、17项其他贡献以及198篇文章的历年引用数。

眼光、坚持、力量

杨振宁是二十世纪后半叶理论物理大师，具有极其鲜明独特的研究风格和品味。他曾经总结自己工作的三个要素 [2]：眼光（perception）、坚持（persistence）、力量（power）。
杨振宁粒子物理唯象工作的特点可以小结如下。杨振宁和合作者脚踏实地，运用对称原理，立足实验分析，提出未来实验方向，而不随便猜测，体现了费米的影响。例如，和李政道提出中微子二分量理论时，在有实验证据之前不随便猜测，而有了实验证据后透彻讨论；和吴大峻分析CP不守恒时，没有理会脱离实际的理论猜测，而作了CP不守恒的唯象分析，集中于未来实验的仔细分析，建立了分析此类现象的唯象框架。这些工作与实验密切联系，引领了本领域发展，大多成为标准知识，进入教科书，人们一般不引用原文了。因为科研新发展，部分文章近年来引用又开始明显增加。
杨振宁统计力学（含多体和凝聚态理论）工作的特点可以小结如下。杨振宁和合作者对扎根于物理现实的普遍模型严格求解与分析，从而漂亮地抓住问题的本质和精髓。这方面工作与物理现象、场论和数学都有深刻联系，对称性也起了重要作用。大多数工作具有极长的生命力，原文引用不断创新高。
无论是场论与粒子物理，还是统计力学与凝聚态物理，杨振宁的研究工作都体现了他对物理学理论的美的追寻，一方面与实验事实紧密相关，一方面又注重物理学的基本结构和理论形式的优美。这种追求和特征贯穿了他的整个研究生涯。从学生时代直到现在，杨振宁总是有独立的思想、想法和直觉，做研究不赶时髦、不随大流、不落俗套，而是独立思考，从物理现象和从自己的物理思想出发，作出深刻的发现，展示物理之美。
杨振宁伴随并深刻影响了二十世纪后半叶物理学的发展。他有些工作的重要性因为得到实验支持很快被承认，很多粒子物理唯象工作属于这种情况，最著名的例子是关于弱相互作用中宇称不守恒的工作；而有些工作的重要性经过很多年以后才被其他物理学家接受，成为相关领域的奠基石，最著名的例子就是杨-米尔斯理论；也有些工作的重要性是越来越多地逐步显示出来，统计力学中很多工作都是如此，包括相变理论和杨-巴克斯特方程。因为醉心于自己的追求，杨振宁会把一时还不能完善或尚未显示出重要性的想法放在一边，等待时机成熟。他将论文选进《选集》时，也不单纯以物理重要性为标准。正所谓 “文章千古事，得失寸心知”。
1954年，杨振宁和米尔斯从物理结构出发提出杨-米尔斯理论时，虽然知道这是一个极美的理论，但当时并没有意识到它如此重要，更不了解规范场的几何意义。杨振宁是物理学家，不是数学家，是从物理现象归纳基本理论，而这些基本理论的结构需要用数学表达。在追寻物理理论的美的过程中，他扎根于物理现实。但他又具有高超的数学能力，能够欣赏数学之美。
在杨振宁的13项重要贡献中，三分之二以上是关于物理现象与代数或几何的对称性之间的关系，包括杨-米尔斯理论。在另外列出的19项贡献中，情况也是类似。统计力学很多工作中，对称性也起了重要作用。这表明了在杨振宁的思考中，对称性占据中心地位。1999年，在石溪的一次学术会议上，杨振宁被称为 “对称之王（Lord of Symmetry）” [6]。
杨振宁着重追寻 “物” 之 “理”，设计物理学的基本理论结构，但他又深刻地认识到实验现象是物理学之根本，十分关注新的实验发现，富有成效地同实验物理学家互动，对物理学各个领域保持兴趣，包括一些看似较 “小” 但反映了物理学精神的问题，比如超导环磁通量子化和AB效应实验验证，从中提炼出美妙的物理，而对一些研究 “大” 问题但猜测性太强的领域不感兴趣。这些特征显然是受到费米的影响。杨振宁从费米那里学到，物理从近距离开始才能得到大的规律，抽象化应在具体工作之后，应该将大部分时间用于简单的实际问题 [2]。
1970年代后，凝聚态物理的实验新发现层出不穷，而高能物理的进步则倚赖于加速器的发展，因此他对凝聚态物理和加速器物理这两个领域特别关注，并鼓励青年人进入这些领域 [2,4,16]。
杨振宁的风格和品味中很多成分出自多年前埋下的 “小的种子”（seedling）[6]。他对对称性的爱好与他天生的气质和幼时的经历不无关系，又与本科生阶段的学习密切相关。而统计力学的研究则起源于硕士论文。在很多工作中表现出的数学能力和对数学美的欣赏，与少年时期对数学的接触分不开。受费米的影响，杨振宁又对很多领域保持兴趣。

杨-米尔斯理论的后续发展

1954年杨-米尔斯理论的原始论文最后一段写道：“在电动力学中，人们认为，电荷守恒要求光子质量消失。对于b场（即杨-米尔斯规范场），没有相应的论证，虽然同位旋守恒成立。因此我们对于b量子（即杨-米尔斯规范粒子）不能做出任何结论。” [3]
这段话颇有预见性。后来发现，杨-米尔斯规范粒子的质量确实可能不为零，也可能为零。对称性自发破缺在保持物理定律的对称性前提下，允许现象的对称破缺，这导致弱相互作用的规范粒子质量。而描述强相互作用的量子色动力学中，规范对称没有破缺，规范粒子胶子的质量确实为零，但是夸克和胶子被禁闭着。
对于对称性自发破缺机制，杨振宁曾经评论道 [2]：“自发破缺的观念既解决了规范粒子的质量问题，又没有破坏对称精神。”
标准模型的建立是多位理论物理学家努力的成果，他们因此获得诺贝尔奖。下面摘录一些诺贝尔演讲。
1979 年诺贝尔奖是关于建立在杨-米尔斯理论基础上的电弱统一理论。
格拉肖（Sheldon Glashow）说：“今天我们有个被称作基本粒子物理学的‘标准理论’，其中强、弱和电磁相互作用都从局域对称原理给出……这个概念在1954年被用到非阿贝尔局域对称群。”
温伯格说：“更复杂的群的推广是1954年杨和米尔斯一篇重要文章中做出，他们展示了怎样构造一个强相互作用的SU(2)规范理论……我们目前关于基本粒子相互作用的细节性理论可以作为对称原理和对付无穷大的可重正化原理的后果。”
1999年诺贝尔奖是关于杨-米尔斯理论的可重正性。
韦尔特曼说：“杨-米尔斯理论大概是对于重正化来说最好的理论……从探究杨-米尔斯理论中的费曼图开始，我确定了很多发散的消失。”
特·胡夫特（Gerard ‘t Hooft）说：“我计算了场论的标度性质，我尝试的第一个理论是杨-米尔斯理论……量子色动力学是一种规范群SU(3)的杨-米尔斯理论。” 特·胡夫特也发现了渐近自由，但是没有发表。
2004年诺贝尔奖是关于杨-米尔斯理论的渐近自由。
格罗斯（David Gross）说：“特·胡夫特关于杨-米尔斯理论可重正性的杰出工作将非阿贝尔规范理论重新介绍到业内……我们判断可以计算杨-米尔斯理论的β函数……”
维尔切克说：“我们发现展示渐近自由的理论叫做非阿贝尔规范理论，或者杨-米尔斯理论（杨和米尔斯，1954）。”
戴森对杨-米尔斯理论作过很多评论 [4,5]：
● “非阿贝尔规范场的发现打下新的知识结构基础，这个知识结构的建造花费了30年。现代理论描述，又被现代实验证实，物质的状态是非阿贝尔规范场的汤，这些规范场由杨振宁45年前发现的数学对称性聚集在一起。” ●“杨振宁占据了外尔的位置，成为我这一代物理学家的领头鸟……杨振宁还画龙点睛地指出，爱因斯坦引力理论符合同一个框架……非阿贝尔规范场生成非平庸的李代数，场之间的相互作用形式被唯一地确定下来，因此对称性支配相互作用。这个想法是杨振宁对物理学最大的贡献。” ●“杨-米尔斯规范场是狄拉克方程之后，理论物理最重要的发现。”




杨-米尔斯理论也带来一系列数学进展：
● 阿蒂亚（M. Atiyah）研究了瞬子解分类，与希钦（N. Hitchin）和辛格（I. Singer）计算了瞬子模空间的维数。● 乌伦贝克（K. Uhlenbeck）将杨-米尔斯方程表示成椭圆系统，导致一系列结果（ 2019 阿贝尔奖成果一部分）。● 陶布思（C. Taubes）研究瞬子模空间边界和自对偶4 维流形的粘结。● 唐纳森（S. Donaldson）在前面三人工作基础上，用瞬子模空间研究4维微分流形拓扑，得到唐纳森定理。结合Freedman定理，说明存在一种4维可微流形，与4维欧几里得空间拓扑等价却不微分等价（1986菲尔兹奖）。 ● 威腾（E. Witten）用超对称杨-米尔斯理论研究低维拓扑等数学问题。
阿蒂亚说：“1977年以后我的兴趣转向规范理论以及几何与物理的相互作用……辛格告诉我杨-米尔斯方程，通过杨振宁的影响，它正在向数学圈渗透。” [17]
乌伦贝克说：“杨-米尔斯方程正等着被发现。但是数学家不能自己创造它们。规范场论是个领养的孩子。物理学家杨和米尔斯于1954年写下他们的方程。” [18]
杨振宁开启了物理与数学前沿两个汇合点，大大促进了数学与物理学以后的成功合作：● 杨-米尔斯理论● 杨-巴克斯特方程
有多位菲尔兹奖获奖工作与杨-巴克斯特方程或杨-米尔斯理论有密切的关系，这两者之间的深刻联系也越来越多地被揭示出来。
杨振宁感怀：“我的大多数物理同事对数学采取实用主义的态度。也许因为我父亲的影响，我对数学有更多的欣赏。我欣赏数学家的价值判断，我崇尚数学的美和力量：既有战术操纵上的机智和复杂，也有战略行动上的激动人心的扫荡。而且，当然，奇迹中的奇迹，数学中一些概念竟提供了主宰物理宇宙的基本结构！” [3]

物理定律的定律

1979年，在纪念爱因斯坦百年寿辰的演讲中，杨振宁总结了 “对称支配力量”（或者 “对称性支配相互作用”）总原理 [3]。
杨振宁梳理，在爱因斯坦提出的狭义相对论基础上，闵可夫斯基最早发现了对称性原理：物理定律必须满足在洛伦兹变换下的不变性。广义相对论基于洛伦兹不变性到广义坐标不变性的推广。
爱因斯坦从广义坐标不变性决定了引力场方程，确定了未知的引力定律。因此，爱因斯坦通过广义相对论开启了 “对称性支配相互作用” 这个原理。
外尔最初试图推广广义相对论，统一引力和电磁力。后来他将规范变换修改为量子力学中的相位变换，从阿贝尔规范不变性确定了电磁定律，虽然当时电磁定律已经是已知的。
杨-米尔斯理论提出时，是作为外尔的电磁规范理论的推广，从非阿贝尔规范不变性确定未知的新的相互作用定律。
所以，4种基本相互作用都由对称性决定。引力由广义相对论描述，其它3种力直接主宰物质微观结构，由杨-米尔斯理论描述。杨-米尔斯理论是二十世纪理论物理三个主旋律交融和变奏的高潮。
特·胡夫特说: “规范理论成为基本粒子理论的中枢概念，并被期待在更基本的理论构造中扮演同样必要的角色，以提供普适物理定律的包容一切的图像。” [19]
因此，今天可以清楚地看到：(1) “对称性支配相互作用” 这个论断简洁地抓住了过去半个世纪理论物理主要的概念性进展， (2) 这个论断将继续为理论物理的进步提供一般性指导。
我称之为物理定律的定律（Law of laws）。
“对称性支配相互作用” 使得主宰世界的基本规律别无选择，成为必然，可以被确定，消除了任意性。也就是说，在深层次的规律上，美就是真，真就是美，美支配真，通过美确定真。当然，要通过实验检验。这是人类思想史上极其深刻的一笔。可谓是大美至真！
格罗斯说：“对称性支配相互作用而杨振宁支配对称性。” [10]
杨振宁曾经回顾1954年的价值判断：“（A）规范不变性的美和力量，以及（B）规范玻色子的质量问题。对于米尔斯和我来说，中心动机来自（A），正如我们的短摘要所表明的。至于（B），米尔斯和我探讨了各种可能性，在我们1954年的文章最后总结道：‘因此我们没有得到关于b 量子的质量的任何结论。’也就是说，我们将（B）当作未来的问题。”
杨-米尔斯理论非常美，然而提出时，规范粒子质量问题没有解决，没有直接的实验支持。但是从非阿贝尔规范不变性得到相互作用，是杨-米尔斯理论的核心思想，是美和力量，是正确的。规范粒子质量问题后来得到了解决。粒子物理标准模型的成功证实了杨振宁基于美的眼光、判断和勇气。这是物理学历史的幸运。
谈到历史，我们可以从哥白尼的日心说得到教益。哥白尼日心说的核心思想是，所有行星绕日运动。由此自然地解释了托勒密地心说中很多奇怪的规定。这是一个大美。
哥白尼日心说的优点在于美，但是它并不比托勒密的地心说更符合观测。它甚至也借用托勒密的方法，如偏心和本轮。日心说在对观测符合上的优势，要等到伽利略基于望远镜的发现。而基于正圆的理论缺陷，要等到开普勒的椭圆轨道来消除。
然而哥白尼日心说的核心思想是正确的，其他问题后来解决。我们还可以看到，圆对称（甚至扩大为球对称）转移到深层次的牛顿引力定律，而轨道形状由于自发对称破缺而成为椭圆。这在细节上也与杨-米尔斯理论有类似。
500年前的哥白尼日心说，今天依然重要，核心思想的重要性和正确性更清楚。可以期待，杨-米尔斯理论500年后也将重要，核心思想的重要性和正确性也会更清楚。
“对称性支配相互作用” 原理的历史脉络是：
爱因斯坦—外尔—杨振宁
这三位关键人物与戴森曾同时是普林斯顿高等研究院的同事，虽然杨振宁没有与爱因斯坦和外尔讨论过这个问题 [1,2,3]。杨-米尔斯理论完美诠释了研究院院徽（图13）所表达的美与真的理念。那是研究院创办者弗莱科斯纳（Abraham Flexner）从济慈（John Keats）的诗受到的影响：
美即是真，真即是美（Beauty is truth, truth beauty）
图13 普林斯顿高等研究院的院徽

参考文献：（上下滑动可浏览）

[1] Yang C N. Selected Papers Ⅱ With Commentaries. World Scientific Publishing Co. Pte. Ltd., 2013[2] 杨振宁(著). 张奠宙(编). 杨振宁文集. 上海: 华东师范大学出版社，1998。[3] Yang C N. Selected Papers 1945—1980 With Commentary. W. H. Freeman and Company Publishers, 1983; 2005 Edition, World Scientific Publishing Co. Pte. Ltd., 2005 [4] Goldhaber A, Shrock R, Smith J, Sterman G, van Niuwenhuizen P, Weisberger W. (Ed.), Symmetry and Modern Physics. World Scientific Publishing Co. Pte. Ltd., 2003. [5] Dyson F. Birds and Frogs (Selected Papers, 1990–2014) (World Scientific, Singapore, 2015. [6] 施郁. 物理学之美：杨振宁的13项重要科学贡献，物理, 43卷, 1期, 57-62 (2014)，https://mp.weixin.qq.com/s/V83_cwtPLoLSSkTc4nd8VQ；增补版，http://blog.sciencenet.cn/blog-4395-836721.html， https://mp.weixin.qq.com/s/EobbROa-rsMEvEfn6bTv0g，收入《诺贝尔奖得主与名人在新加坡南洋理工大学讲演与访谈》，2016；Beauty and Physics: 13 important contributions of Chen Ning Yang, Int. J. Mod. Phys. A 29, No. 17, 1475001 (2014)；Brief overview of C. N. Yang’s 13 important contributions to physics, Int. J. Mod. Phys. A 30, No. 36, 1530069(2015)。[7] M. Brown, M. Dresden and L. Hoddeson (ed.), Pions to Quark, Cambridge University Press, 1989.[8] Steinberger J. Learning about Particles – 50 Privileged Years. Springer, 2005.[9] Cronin J W (ed.), Fermi Remembered, University of Chicago (2004) P.34. [10] Liu C S , Yau S T. (Ed.). Chen Ning Yang: A Great Physicist of the Twentieth Century. International Press, 1997 [11] Ruelle D. The Mathematician's Brain, Princeton University Press, 2007.[12] Weinberg S. Facing Up: Science and Its Cultural Adversaries Trade. Havard. 2003.[13] Reines F, Cowan C L Jr, Harrison F B, McGuire A D, Kruse H W. 1960. Detection of the Free Antineutrino. Physical Review 117 (1): 159；[14] Reines F. 1979. The Early Days of Experimental Neutrino Physics. Science 203 (4375): 11.[15] Veltman M. Facts and mysteries in elementary particle physics. World Scientific, 2003.[16] Leggett A J. Quantum Liquids. Oxford University Press, 2006. [17] Atiyah M. Collected Works: Volume 5: Gauge Theories. Oxford University Press, 1988.1[18] Uhlenbeck K. Instantons and their Relatives. Proceedings of the AMS Centennial Symposium, 1988.[19] ‘t Hooft G (Ed.). 50 Years of Yang-Mills Theory. World Scientific, Singapore, 2005.
制版编辑 |卢卡斯